컴파일러보다 최적화 잘 하기: Constant Division Strength Reduction

자유주제 세미나의 일환으로 Constant Division 의 Strength Reduction 을 소개하는 시간을 가졌습니다.

나 인턴한 것도 기록해야 하는데 그건 언제하지

---

관찰

int main(void) {
    unsigned int x, y, z;
    z = x/y;
    return 0;
}

 

간단한 C 언어 코드다. 컴파일해보자

gcc -S divxy.c -o divxy.asm

 

다른건 볼 필요 없고 대충 스택에서 두 변수를 가져와서 나누는 것 같다.

이번에는 아래 코드를 컴파일해보자

int main(void) {
    unsigned int x, y, z;
    z = x/3;
    return 0;
}

gcc -S divx3.c -o divx3.asm

 

컴파일 결과가 (사람 기준으로) 이상한 것을 확인 가능하다.

내가 한건 div 인데 왜 mul(multiplication) 이랑 shr(shift right) 이 나올까

이거에 대해서 알아보자. ^[각주:1] 

---

저게 뭘까

Programming Language Design and Implementation

ACM SIGPLAN: ACM Special Interest Group on Programming LANguage

ACM 에는 대략 30여개의 SIG가 있고 그 중 Programming LANguage 를 다루는 SIG 또한 존재한다. 여기서 주최하는 PLDL 이라는 학회가 있다.

2025년에는 서울에서 한 것 같은데, 아무튼.

 

1994년에, PLDL 에서 "Division by Invariant Integers Using Multiplication." 이라는 제목의 페이퍼가 나온다. 엄밀히 말하면 4B 나눗셈 하나를 8B 짜리 곱셈 하나와 rshift 하나로 동치시킬 수 있다는 주제.

나눗셈은 다른 연산에 비해 압도적으로 느리므로, 대치를 통해 높은 속도 향상을 얻을 수 있을 것이다.

---

저게 왜 될까

unsigned 정수 연산에서, 우리가 x / 3 을 계산할 때, 실제로 계산되는 값은 floor( x / 3 ) 이다.^[각주:2] 이 floor( x / 3 ) 값이 다르게 구해질 수 있음을 증명하자. 

 

분모 분자에 같은 값을 곱했으므로 이것 또한 성립한다. 저기서 분수는 정수 나눗셈이 아니라 실제 실수 연산.

 

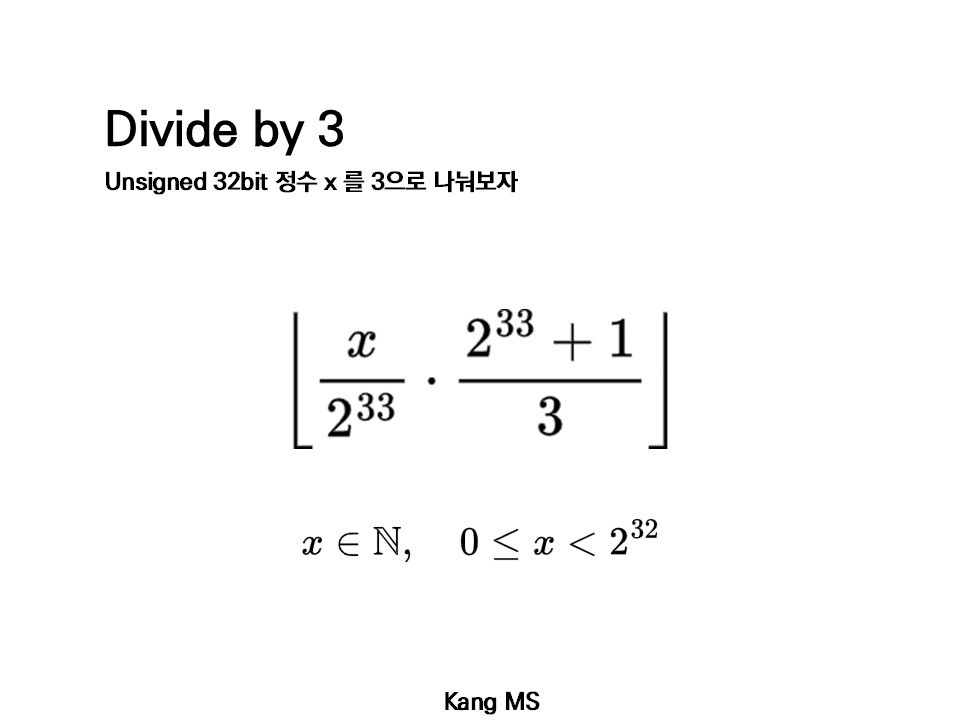
근데 이 값 또한 floor( x / 3 ) 과 같다. 전개하면 우측과 같이 되는데, x / 3 * 2^{33} 이 무조건 1/3 보다 작으므로, 정수 값을 바꿀 힘이 없다.

 

이게 작은 결론

 

근데 이 값은 이렇게 전개할 수도 있는데, 그럼 자명하게 (1 / 2^{33}) 을 밖으로 빼낼 수 있고

2^{33} + 1 은 무려 3과 나누어 떨어지므로, 계산하여 정수 M 으로 치환 가능하다.

 

정수곱은 당연히 정수이므로, floor 를 괄호로 대치할 수 있다.

이로써 정수 div을 mtp + sft 로 대체하는 데 성공하였다.

 

일반화 하면 다음과 같다.

 

가끔식 M 값이 2^32 보다 커지는 경우가 생기는데, 어쨌든 M 이 2^33 보다는 작으므로 우측 사진처럼 보정해주면 정상적으로 사용할 수 있다.

---

어디다가 쓸까

나눗셈을 곱셈으로 대체 가능하다는 아이디어는 상당히 아름다운 편이기에 쓸 수 있는 엥간한 곳에서는 다 쓴다. 심지어 나누는 값이 variant 해도 쓴다.

gcc llvm 에서 쓰이고 있고, gcc 는 -O0 flag 를 켜도 이건 해준다. 이건 최적화 위치랑 관련있는데 뒤에서 설명하겠음

llvm 에서는 -O3 flag 에서부터 적용된다.

다른 사람이 돌려서 기록한 표가 있으니 확인해보면 좋을 듯  

 

 

V8(for chromium), 리눅스 커널에도 쓴다. 앞서서도 봤겠지만 M 값 자체가 계산하기 그렇게 복잡한게 아니기 때문에^[각주:3], 그냥 런타임에서 저장하고 캐시 때린다고 한다.

div 13 명령어가 들어오면, 13에 대응하는 M 값을 계산 한 뒤, 그것으로 나눗셈을 수행. 이후 나중에 div 13 명령어가 다시 들어오면, 계산 되어 있는 M 값으로 나눗셈 수행.

 

이런 식

---

코드에서 사용하기

정수 최적화는 이미 컴파일러가 해주기 때문에 우리가 할 필요는 없다

다만 실수. 실수에서도 비슷한 짓을 할 수 있다.

정확성 증명만 제외하면 1보다 큰 실수에서 비슷한 짓을 수행할 수 있으므로, 해당 과정을 그대로 적용할 수 있다.

 

정수에서 pi 를 나눈 값을 정수로 반환하는 invpi 함수를 생각하자.

#define INV_PI = "INVERSION_VALUE_OF_PI"
inlint int invpi(int x) { return x * INV_PI; }

 

이렇게 짜면 int-double 형변환 / 부동실수곱 / double-int 형변환 이 각각 한 번씩 수행된다.

형변환이 두 번이나 있어서 예쁘지 않다

 

 

이렇게 대치할 수 있다.

첫 번째의 경우, 파이를 소수점 9자리까지 근사한 것이 되고, 이에 따라서 -1 ~ +1 수준의 오차가 발생가능하다.

모든 unsigned int 32 에 대해 작동하지만, 최초 오차가 104348 에서 등장한다.^[각주:4]

 

만약 오차가 발생하는 것이 마음에 들지 않는다면, 두 번째 사진처럼도 대치할 수 있다.

이 경우 pi 값을 소수점 12자리까지 근사하게 되고 (...35897932... 를 ...35909870... 로 근사), 5,419,350 까지 exact value 를 반환한다.

다만, 이 경우 x 가 24bit 범위를 넘어가는 순간부터 overflow 에 의하여 아예 다른 값이 나오게 된다.

 

이런 식으로 계산하는게 대략 8배 정도 빠르다

[Source] 서울대학교 시스템 프로그래밍 채점 서버

실제 벤치마크 결과. 부동소수점곱이 대충 34ms 걸리고 SR 이 4ms 정도 걸렸으니 얼추 맞는다.

---

결론

근데 더러운건 사실이니 간 보면서 적당히 씁시다.

학교 과제에 이런거 쓰면 좀 어색하죠

---

TMI

이런 이야기를 할 수 있습니다.

먼저 엥간한 최적화는 다 끄는 gcc -O0 flag 에서도 해당 Strength Reduction 이 시행되는 이유는, 해당 최적화 path 가 다른 최적화들과 달리 backend 에서 발생하기 때문입니다. 엄밀히는 벡엔드 직전의 RTL expansion 에서 발생하며, 이때문에 다른 최적화와 달리 O0 에서도 적용됩니다.

 

다른 이야기로는, 생략한 signed value 에서의 SR 값 정합성 보장 등이 있습니다만, 생략하도록 하겠습니다.

궁금한 분들은 아래 pdf 참고하시면 되겠습니다.

division_is_mtp.pdf

2.15MB

1. 참고로 저 값이 2^64에서 3의 모듈러 곱 역원인데, 이건 우연이다. 우연이 아닌걸 보고 싶으면 7로 비슷한 짓을 해보면 알 수 있다 [본문으로]
2. 단, divisor 가 음수일 경우는 ceil(x / -3) 이 된다. 여기서는 음수는 다루지 않는다 [본문으로]
3. 이론상 나눗셈 한 번에 나머지 연산 한 번이면 계산 가능 [본문으로]
4. 여담이지만 104348/33215 가 꽤 뛰어난 pi 근사값이다 [본문으로]