Plane sweep algorithm

Plane sweep algorithm은 서로 겹치는 직사각형들이 주어질때, 직사각형이 총 차지하는 면적을 구하는 문제에 주로 사용됩니다. 아래 기술하는 알고리즘이 완벽한 plane sweep algorithm은 아니자만, 특별한 상황이 아닌 이상 plane sweep algorithm을 사용하는데는 지장이 없을 겁니다. 정확한 plane sweep algorithm은 아래 pdf를 참고해주시면 감사하겠습니다.

plane sweep algorithm1 (sweepline).pdf

0.20MB

plane sweep algorithm2 (sweepline).pdf

0.57MB

---

아래 직사각형이 겹쳐졌을때 총 넓이를 구한다 가정해봅시다.

 

먼저 직사각형의 가로선들을 포함하는, x축에 평행한 직선들을 추출해냅니다.

 

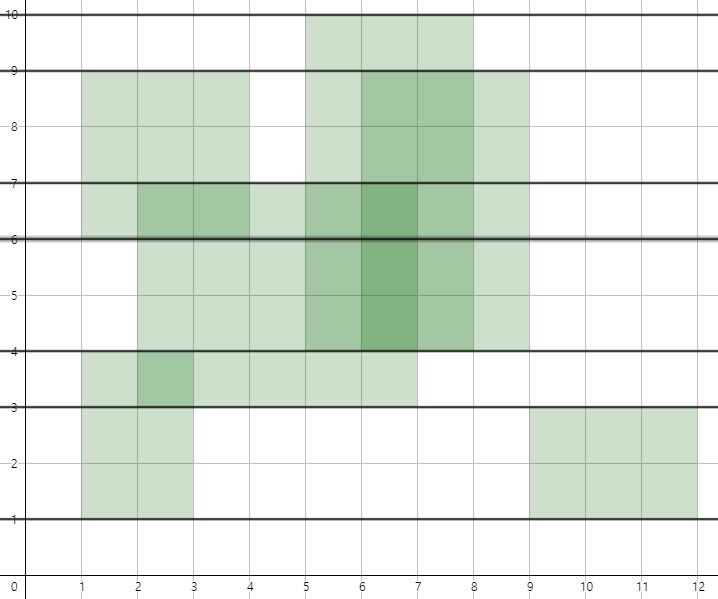
직사각형의 가로선들로 Y[]배열을 만듭니다.
배열을 만들어낸 후에는, 오름차순으로 정렬하고, 중복된 값들을 제거하여 Y[]배열을 완성합니다.

Y[0]	Y[1]	Y[2]	Y[3]	Y[4]	Y[5]	Y[6]
1	3	4	6	7	9	10

이후 Y[]배열과 같은 길이를 가지는 O[]배열도 반듭니다. O[]배열은 두 개의 값을 가지는 pair를 자료형으로 가지는데,

첫 번째 값은 범위 내의 x 시작 좌표, 두 번쨰 값은 계산에 도움이 되는 정수입니다. 두 번쨰 값은 cur라 부르겠습니다. 
이떄 말하는 O[i]의 범위는 y좌표 Y[i] ~ Y[i-1]까지의 범위입니다.

	O[0]	O[1]	O[2]	O[3]	O[4]	O[5]	O[6]
X start cor	0	0	0	0	0	0	0
cur	0	0	0	0	0	0	0

마지막으로, 직사각형의 세로선들로 X[]배열을 만듭니다.
X[]배열은 조금 복잡한데, 네 개의 값을 가지는 pair <pair, pair> 자료형으로 가집니다.
첫 번쨰 값은 선분의 x좌표, 두 번쨰 값은 선분이 직사각형의 왼쪽 세로선(open 선분)인지 오른쪽 세로선(close 선분)인지의 여부, 세 번째 값은 선분의 상단 Y좌표, 네 번쨰 값은 선분의 하단 Y좌표입니다.

*저는 open선분은 1, close선분은 0으로 여부를 표시했습니다. 이 둘을 구분하게 하는 값은 어느것이든 상관은 없지만, open선분을 나타내는 값이 close선분을 나타내는 값보다는 커야 합니다.

 

Y[]와 마찬가지로 배열을 만든후, 정렬해서 완성합니다. (단, 중복된 선분은 제거하지 않습니다.)
X[i]의 범위는 y좌표 y lower cor ~ y upper cor까지의 범위입니다.

	X[0]	X[1]	X[2]	X[3]	X[4]	X[5]	X[6]	X[7]	X[8]	X[9]	X[10]	X[11]
x cor	1	1	2	3	4	5	6	7	8	9	9	12
open/close	1	1	1	0	0	1	1	0	0	0	1	0
y upper cor	4	9	7	4	9	10	9	7	10	9	3	3
y lower cor	1	6	3	1	6	4	4	3	4	4	1	1

 그럼 계산을 위한 모든 준비는 끝난겁니다.
sweep을 왼쪽부터 오른쪽으로, 즉 배열 index 0부터 훑어가며 아래 과정을 계산합니다.

sum을 0으로 초기화
for문 내에서 직사각형의 세로선 하나를 지정하고(X[i]), 아래를 수행한다 | (X[i])
	X[i]의 범위의 시작점을 나타내는 O[]의 인덱스(j)를 구한다 | (j)
	만약 X[i]가 open/left 선분이라면 아래를 수행
		O[i]의 cur이 0이라면 x start cor을 X[i]의 x cor로 대입
		범위에 속하는 모든 O[]의 요소의 cur을 1증가시킴
	아니라면 아래를 수행
		범위에 속하는 모든 O[]의 요소의 cur을 1 감소시킴
		O[i]의 cur이 0이라면 sum에 (x cor - x start cor) * (Y[i] - Y[i-1])의 값을 더한다.
sum이 직사각형들의 총 넓이

 

이로써 최종적인 값을 구할 수 있게 되는 겁니다.
아래의 코드를 참고해 보신다면 이해에 도움이 될것입니다.

---

백준 알고리즘에 등재되어있는 plane sweep algorithm문제는 아래와 같습니다.

https://www.acmicpc.net/problem/2672

2672번: 여러 직사각형의 전체 면적 구하기

plane sweep algorithm을 이용한 답은 아래와 같습니다.

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

// y cor
vector<int> Y;
// y open x cor, cur | Y[i-1] ~ Y[i] -> O[i]'s range
vector< pair <int, int > > O;
// x cor, open / close, y upper cor, y lower cor
vector< pair< pair<int, int>, pair< int, int > > > X;

enum { close, open }; // open should be bigger than close

void regist(int x1, int x2, int y1, int y2) {
	Y.push_back(y1); Y.push_back(y2);
	X.push_back(make_pair(make_pair(x1, open), make_pair(y1, y2)));
	X.push_back(make_pair(make_pair(x2, close), make_pair(y1, y2)));
}

void sorting(void) {
	sort(Y.begin(), Y.end());
	Y.erase(unique(Y.begin(), Y.end()), Y.end());
	O.resize(Y.size());
	sort(X.begin(), X.end());
}

int calculating(void) {
	int Xsize, Ysize, j;
	int sum = 0;
	Xsize = X.size(); Ysize = Y.size();
	for (int i = 0; i < Xsize; i++) {
		for (j = 0; j < Ysize; j++) { if (Y[j] >= X[i].second.first) { j++; break; } }
		if (X[i].first.second == open) {
			for (; j < Ysize; j++) {
				if (!O[j].second) { O[j].first = X[i].first.first; }
				O[j].second++;
				if (Y[j] >= X[i].second.second) { break; }
			}
		}
		else {
			for (; j < Ysize; j++) {
				O[j].second--;
				if (!O[j].second) { sum += (Y[j] - Y[j - 1]) * (X[i].first.first - O[j].first); }
				if (Y[j] >= X[i].second.second) { break; }
			}
		}
	}
	return sum;
}

int main(void) {
	int N;
	double sx, sy, rx, ry;
	int V;
	cin >> N;

	for (int i = 0; i < N; i++) {
		cin >> sx >> sy >> rx >> ry;
		sx *= 10; sy *= 10; rx *= 10; ry *= 10;
		regist(sx, sx + rx, sy, sy + ry);
	}
	sorting();
	V = calculating();
	if (!(V % 100)) cout << V / 100; 
	else { printf("%.2f", V / 100.0); }
	return 0;
}

이상으로 KMS studio였습니다.